Quant Developer, we look at constructing, pricing and reporting on Inverse Floater derivatives in C# using opengamma strata.

We, at poc-d, have taken opengamma‘s strata library (which has been developed in java) and extended it for online learning of capital market products for C#, VB.Net, C++, Python, Java and Scala developers as well an Microsoft Excel addin for financial analysts.

The learning is hands on, which means you will be provided a copy of the library to follow along.

Course Curriculum

• Module #1 : Fixed/Float Swap Structure
  • xxx
  • xxx
  • xxx
• Module #2 : Fixed/Float Swap Pricing
  • xxx
  • xxx
  • xxx
• Module #3 : Fixed/Float Swap FpML
  • xxx
  • xxx
  • xxx
  • xxx
• Module #4 : Fixed/Float Swap Risks
  • xxx
  • xxx
  • xxx

• Provided (for hands on)
  • Microsoft Excel Addin which exposes required opengamma strata financial functions within Excel
  • .NET assembly in which to write capital market code against
• Required
  • Minimum Microsoft Windows 7
  • 4GB of RAM (8GB preferred)
  • Visual Studio 2010 onwards for .NET Development (You can install the free version of Visual studio 2015 community)
  • Optional : Microsoft Excel 2007 onwards

Course Access

This course is broken down into modules (as seen in the graphic above).

You can access all the Capital Market courses based on C#, VB.Net, C++, Python, Java, Scala and Microsoft Excel for one low monthly fee. Currently the membership site houses courses that covers Fixed Rate Bonds, Swaps, Inverse Floaters, Swaptions and Cap/Floors.

• POC-d membership site : POC-D Membership site

Or each module can be purchased individually from

• Udemy : POC-D Udemy Individual modules

Fixed/Float Swap Derivative

In an interest rate swap, each counterparty agrees to pay either a fixed or floating rate denominated in a particular currency to the other counterparty. The fixed or floating rate is multiplied by a notional principal amount (say, $1 million) and an accrual factor given by the appropriate day count convention. When both legs are in the same currency, this notional amount is typically not exchanged between counterparties, but is used only for calculating the size of cashflows to be exchanged. When the legs are in different currencies, the respective notional amounts are typically exchanged at the start and the end of the swap, which is called cross currency interest rate swap.

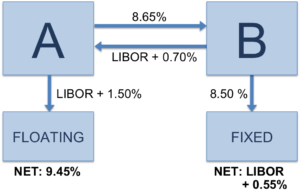
Party A is currently paying floating rate, but wants to pay fixed rate. Party B is currently paying fixed rate, but wants to pay floating rate. By entering into an interest rate swap, the net result is that each party can swap their existing obligation for their desired obligation.

The most common interest rate swap involves counterparty A paying a fixed rate (the swap rate) to counterparty B while receiving a floating rate indexed to a reference rate like LIBOR, EURIBOR, or MIBOR. By market convention, the counterparty paying the fixed rate is the “payer” (while receiving the floating rate), and the counterparty receiving the fixed rate is the “receiver” (while paying the floating rate).

A pays fixed rate to B (A receives floating rate)

B pays floating rate to A (B receives fixed rate)

Currently, A borrows from Market @ LIBOR +1.5%. B borrows from Market @ 8.5%.

Consider the following swap in which Party A agrees to pay Party B periodic fixed interest rate payments of 8.65% in exchange for periodic variable interest rate payments of LIBOR + 70 bps (0.70%) in the same currency. Note that there is no exchange of the principal amounts and that the interest rates are on a “notional” (i.e., imaginary) principal amount. Also note that interest payments are settled in net; that is, Party A pays (LIBOR + 1.50%)+8.65% – (LIBOR+0.70%) = 9.45% net. The fixed rate (8.65% in this example) is referred to as the swap rate.^[2]

At the point of initiation of the swap, the swap is priced so that it has a net present value of zero. If one party wants to pay 50 bps above the par swap rate, the other party has to pay approximately 50bps over LIBOR to compensate for this.

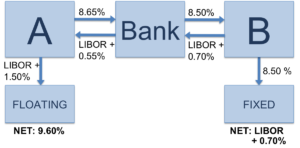
Normally the parties do not swap payments directly, but rather each sets up a separate swap with a financial intermediary such as a bank. In return for matching the two parties together, the bank takes a spread from the swap payments (in this case 0.30% compared to the above example)

Interest rate swaps are used to hedge against or speculate on changes in interest rates.

Speculation

Interest rate swaps are also used speculatively by hedge funds or other investors who expect a change in interest rates or the relationships between them. Traditionally, fixed income investors who expected rates to fall would purchase cash bonds, whose value increased as rates fell. Today, investors with a similar view could enter a floating-for-fixed interest rate swap; as rates fall, investors would pay a lower floating rate in exchange for the same fixed rate.

Interest rate swaps are also popular for the arbitrage opportunities they provide. Varying levels of creditworthiness means that there is often a positive quality spread differential that allows both parties to benefit from an interest rate swap.

The valuation of vanilla swaps was often done using the so-called textbook formulas using a unique curve in each currency. Some early literature described some incoherence introduced by that approach and multiple banks were using different techniques to reduce them. It became even more apparent with the 2007–2012 global financial crisis that the approach was not appropriate. The now-standard pricing framework is the multi-curves framework.

The present value of a plain vanilla (i.e., fixed rate for floating rate) swap can be computed by determining the present value (PV) of the fixed leg and the floating leg.

The value of the fixed leg is given by the present value of the fixed coupon payments known at the start of the swap

The value of the floating leg is given by the present value of the floating coupon payments determined at the agreed dates of each payment. However, at the start of the swap, only the actual payment rates of the fixed leg are known in the future, whereas the forward rates are unknown. The forward rate for each floating payment date is calculated using the forward curves.

During the life of the swap the same valuation technique is used, but since, over time, both the discounting factors and the forward rates change, the PV of the swap will deviate from its initial value. Therefore, the swap will be an asset to one party and a liability to the other.

Interest rate swaps expose users to many different types of financial risk^[7]

Predominantly they expose the user to market risks. The value of an interest rate swap will change as market interest rates rise and fall. In market terminology this is often referred to as delta risk. Other specific types of market risk that interest rate swaps have exposure to are basis risks (where various IBOR tenor indexes can deviate from one another) and reset risks (where the publication of specific tenor IBOR indexes are subject to daily fluctuation). Interest rate swaps also exhibit gamma risk whereby their delta risk increases or decreases as market interest rates fluctuate.

The text below is an edited version taken from the strata web site : http://strata.opengamma.io/introduction/

Introduction to Strata for the Quant Developer

What is Strata?

Strata is the award-winning open source analytics and market risk library from OpenGamma.

Strata allows quant developers to build or enhance existing applications with standardized, off-the-shelf market risk components. It includes:

• Pricing, financial analytics and curve calibration
• Reporting
• Scenario evaluation
• Trade modelling
• Market data representation
• Financial foundations – currencies, indices, holidays, date adjustments, schedules, time-series

Strata has been built from the ground up to be lightweight and flexible. It does not impose any database, server or middleware requirements; these would be built on top of Strata. It provides a high-quality, open source Java toolkit that is designed to be used both in its entirety, as well as for its individual components.

Who is Strata for?

Firms have long employed expensive resources – quants and quant developers – to build and maintain market risk functionality that  offers no real competitive advantage. Where possible, they wish to leverage existing investments in systems and other in-house technologies, while looking externally for just the components required to fill their solution gaps.

Is there an alternative?

One alternative to building in-house is to look towards out-of-the-box offerings provided by financial software vendors. While these vendors offer solutions to industry business issues, the downside is that many firms have been burned by opaque, closed source vendor models, including vendor lock-in to make or support any changes, and “sledgehammer to crack a nut” software footprints.

Solution

Strata delivers the best of both worlds – industry standard market risk functionality, distributed as open source java software to eliminate vendor dependency and return control back to in-house development teams. With open access to standard market risk components and java source code, firms can accelerate the time-to-market of their solutions.

Developers

Strata is aimed at quant or systems developers tasked with delivering analytic solutions into trading, risk, clearing or prime servicing, or collateral businesses. Strata empowers developers with vetted open source java components that deliver standard market risk functionality, allowing them to focus on the unique aspects of solutions delivery to their business stakeholders.